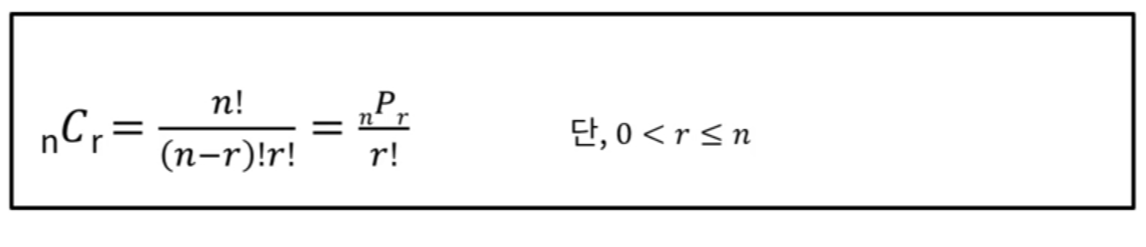
조합(Combination)
서로 다른 n개 중에서 r개를 선택하는 경우의 수(순서X, 중복X)
-예시) 서로 다른 4명 중 주번 2명 뽑는 방법
중복 조합
서로 다른 n개 중에서 r개를 선택하는 경우의 수(순서X, 중복O)
-예시) 후보 2명, 유권자 3명일 때 무기명 투표 방법

// 기초 수학 - 조합
public class Main {
static int getCombination(int n, int r) {
int pResult = 1;
for (int i = n; i >= n - r + 1; i--) {
pResult *= i;
}
//r팩토리얼
int rResult = 1;
for (int i = 1; i <= r; i++) {
rResult *= i;
}
return pResult / rResult;
}
public static void main(String[] args) {
// 1. 조합
System.out.println("== 조합 ==");
//서로 다른 4명 중 주변 2명 뽑는 경우의 수
int n = 4;
int r = 2;
int pResult = 1;
for (int i = n; i >= n - r + 1; i--) {
pResult *= i;
}
//r팩토리얼
int rResult = 1;
for (int i = 1; i <= r; i++) {
rResult *= i;
}
System.out.println("결과 : " + pResult / rResult);
//결과 : 6
// 2. 중복 조합
System.out.println("== 중복 조합 ==");
//후보 2명, 유권자 3명일 때 무기명 투표 경우의 수
n = 2;
r = 3;
System.out.println("결과 : " + getCombination(n + r - 1, r));
//결과 : 4
}
}
// Practice
// 1, 2, 3, 4 를 이용하여 세자리 자연수를 만드는 방법 (순서 X, 중복 x)의 각 결과를 출력하시오
public class Practice {
void combination(int[] arr, boolean[] visited, int depth, int n, int r) {
if (r == 0) {
for (int i = 0; i < n; i++) {
if (visited[i]) {
System.out.print(arr[i] + " ");
}
}
System.out.println();
return;
}
if (depth == n) {
return;
}
visited[depth] = true;
combination(arr, visited, depth + 1, n, r - 1);
visited[depth] = false;
combination(arr, visited, depth + 1, n, r);
}
public static void main(String[] args) {
// Test code
int[] arr = {1, 2, 3, 4};
boolean[] visited = {false, false, false, false};
Practice p = new Practice();
p.combination(arr, visited, 0, 4, 3);
//출력 결과
//1 2 3
//1 2 4
//1 3 4
//2 3 4
}
}
'알고리즘 & 자료구조 > 알고리즘' 카테고리의 다른 글
| 지수와 로그 (0) | 2024.08.05 |
|---|---|
| 점화식(Recurrence)과 재귀함수(Recursive Function) (0) | 2024.08.04 |
| 경우의 수 (0) | 2024.08.04 |
| 집합, 교집합, 합집합, 차집합, 여집합 (0) | 2024.08.04 |
| 순열 (0) | 2024.08.03 |