선형 자료구조 - 데크(Deque)

알고리즘 & 자료구조/자료구조

선형 자료구조 - 데크(Deque)

죽밥죽밥화이팅 2024. 8. 20. 14:14

데크(Deque)

양쪽에서 삽입과 삭제가 모두 가능한 자료구조

-Deque : Doubly-ended Queue

-Stack과 Queue를 합친 형태

Double-Ended Queue"라는 이름에서 알 수 있듯이, 일반적인 큐(Queue)와 유사하지만,

데크는 양쪽 끝에서 연산을 수행할 수 있는 점에서 차별화 됨

주요 특징

양방향 연산: 데크에서는 앞쪽(front)과 뒤쪽(rear) 모두에서 요소를 삽입(insert)하거나 삭제(remove) 가능
유연한 활용: 데크는 큐(Queue)와 스택(Stack)으로 모두 활용할 수 있으며, 특정 상황에서는 양쪽 끝에서의 접근이 필요한 알고리즘에 적합
순서 유지: 데크는 큐와 마찬가지로 삽입된 요소들의 순서를 유지. 따라서, 순서가 중요한 데이터를 관리하는 데 유용

시간 복잡도

삽입 및 삭제: O(1) (양쪽 끝에서의 삽입 및 삭제가 상수 시간에 이루어짐)
접근 및 검색: O(n) (특정 위치에 있는 요소에 접근하거나 검색하려면 전체를 탐색해야 함)

데크의 활용 사례

슬라이딩 윈도우: 슬라이딩 윈도우 기법에서 데크는 일정 구간의 최댓값 또는 최솟값을 빠르게 찾는 데 사용
백트래킹: 스택과 큐의 특징을 동시에 사용할 수 있기 때문에, 백트래킹 문제에서도 유용하게 활용
캐시 구현: 데크는 LRU(Least Recently Used) 캐시를 구현하는 데 사용될 수 있음. 가장 오래된 요소를 앞쪽에서 삭제하고, 새로운 요소를 뒤쪽에 추가하는 방식으로 동작

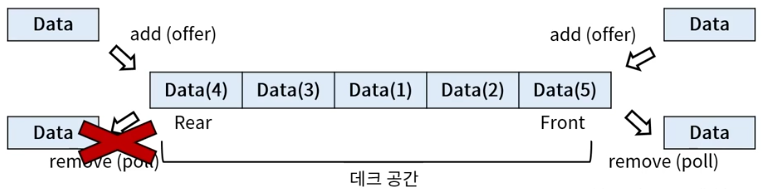
데크 기본 구조

데크의 기본 구조는 양방향에서 삽입 삭제가 가능한 구조

일부 기능을 제한하여 용도에 맞게 변형 가능

Front : 데크의 앞쪽
Rear : 데크의 뒤쪽
add(offer) : 데이터 삽입
remove(poll) : 데이터 삭제

[ add / remove ] 와 [ offer / poll ] 의 차이

데이터를 추가할 공간이 없거나, 꺼낼 데이터가 없을 경우

add / remove => 예외를 발생시킴

offer / poll => null이나 false를 반환시켜주기 때문에 return 값을 받아서 처리가 가능함, 따로 예외처리가 필요함

System.out.println(deque.pollLast()); // null
System.out.println(deque.removeLast()); // 예외 발생

입력제한 데크(Scroll)

한 쪽의 입력을 제한한 데크

출력제한 데크(Shelf)

한 쪽의 출력을 제한한 데크

구현 방법

데크는 배열(Array) 또는 연결 리스트(Linked List)를 이용해 구현될 수 있음

배열 기반 데크: 고정된 크기의 배열을 사용하여 구현할 수 있으며, 배열의 양 끝에서 삽입과 삭제 연산을 수행
연결 리스트 기반 데크: 동적 크기의 연결 리스트를 사용하여 구현할 수 있으며, 양쪽 끝에서의 삽입과 삭제 연산이 효율적

Array를 이용한 데크 구현(원형 구현)

// 배열을 이용한 기본 데크 직접 구현 (원형으로 구현)

class MyDeque2 {
    int[] arr;
    int front = 0;
    int rear = 0;

    MyDeque2(int size) {
        this.arr = new int[size + 1];
    }

    public boolean isEmpty() {
        return this.rear == this.front;
    }

    public boolean isFull() {
        return (this.rear + 1) % this.arr.length == this.front;
    }

    public void addFirst(int data) {
        if (this.isFull()) {
            System.out.println("Deque is Full!");
            return;
        }

        this.arr[this.front] = data;
        // 원형 구조로 만들기 위한 연산
        this.front = (this.front - 1 + this.arr.length) % this.arr.length;
    }

    public void addLast(int data) {
        if (this.isFull()) {
            System.out.println("Deque is Full!");
            return;
        }
        this.rear = (this.rear + 1) % this.arr.length;
        this.arr[this.rear] = data;
    }

    public Integer removeFirst() {
        if (this.isEmpty()) {
            System.out.println("Deque is empty!");
            return null;
        }

        this.front = (this.front + 1) % this.arr.length;
        return this.arr[this.front];
    }

    public Integer removeLast() {
        if (this.isEmpty()) {
            System.out.println("Deque is empty!");
            return null;
        }

        int data = this.arr[this.rear];
        this.rear = (this.rear - 1 + this.arr.length) % this.arr.length;
        return data;
    }

    public void printDeque() {
        int start = (this.front + 1) % this.arr.length;
        int end = (this.rear + 1) % this.arr.length;

        for (int i = start; i != end; i = (i + 1) % this.arr.length) {
            System.out.print(this.arr[i] + " ");
        }
        System.out.println();
    }

}

public class Practice2 {
    public static void main(String[] args) {
        // Test code
        MyDeque2 myDeque = new MyDeque2(5);
        // Front 부분 입력
        myDeque.addFirst(1);
        myDeque.addFirst(2);
        myDeque.addFirst(3);
        myDeque.printDeque();   // 3 2 1

        // Rear 부분 입력
        myDeque.addLast(10);
        myDeque.addLast(20);
        myDeque.addLast(30);    // Deque is full!
        myDeque.printDeque();        // 3 2 1 10 20

        // Front 부분 출력
        System.out.println(myDeque.removeFirst());  // 3
        myDeque.printDeque();   // 2 1 10 20

        // Rear 부분 출력
        System.out.println(myDeque.removeLast());   // 20
        myDeque.printDeque();    // 2 1 10

        System.out.println(myDeque.removeLast());   // 10
        System.out.println(myDeque.removeLast());   // 1
        System.out.println(myDeque.removeLast());   // 2
        System.out.println(myDeque.removeLast());   // Deque is empty!
    }
}

ArrayList를 이용한 데크 구현

// ArrayList 를 이용한 데크 구현

import java.util.ArrayList;

class MyDeque1 {
    ArrayList list;

    MyDeque1() {
        this.list = new ArrayList();
    }

    public boolean isEmpty() {
        if (this.list.size() == 0) {
            return true;
        } else {
            return false;
        }
    }

    public void addFirst(int data) {
        this.list.add(0, data);
    }

    public void addLast(int data) {
        this.list.add(data);
    }

    public Integer removeFirst() {
        if (this.isEmpty()) {
            System.out.println("Deque is empty!");
            return null;
        }

        int data = (int) this.list.get(0);
        this.list.remove(0);
        return data;
    }

    public Integer removeLast() {
        if (this.isEmpty()) {
            System.out.println("Deque is empty!");
            return null;
        }

        int data = (int) this.list.get(this.list.size() - 1);
        this.list.remove(this.list.size() - 1);
        return data;
    }

    public void printDeque() {
        System.out.println(this.list);
    }

}

public class Practice1 {
    public static void main(String[] args) {
        // Test code
        MyDeque1 myDeque = new MyDeque1();
        // Front 부분 입력
        myDeque.addFirst(1);
        myDeque.addFirst(2);
        myDeque.addFirst(3);
        myDeque.printDeque();    // 3 2 1

        // Rear 부분 입력
        myDeque.addLast(10);
        myDeque.addLast(20);
        myDeque.addLast(30);
        myDeque.printDeque();    // 3 2 1 10 20 30

        // Front 부분 출력
        System.out.println(myDeque.removeFirst());  // 3
        myDeque.printDeque();    // 2 1 10 20 30

        // Rear 부분 출력
        System.out.println(myDeque.removeLast());   // 30
        myDeque.printDeque();    // 2 1 10 20

        System.out.println(myDeque.removeLast());   // 20
        System.out.println(myDeque.removeLast());   // 10
        System.out.println(myDeque.removeLast());   // 1
        System.out.println(myDeque.removeLast());   // 2
        myDeque.printDeque(); // []
    }
}

ArrayDeque를 이용한 데크 구현

// 선형 자료구조 - 데크


import java.util.ArrayDeque;
import java.util.Deque;

public class Main {
    public static void main(String[] args) {
        Deque deque = new ArrayDeque();

        // Front 부분 입력
        deque.addFirst(1);
        deque.addFirst(2);
        deque.addFirst(3);
        System.out.println(deque); // [3, 2, 1]

        // Rear 부분 입력
        deque.addLast(10);
        deque.addLast(20);
        deque.addLast(30);
        System.out.println(deque); // [3, 2, 1, 10, 20, 30]

        // Front 부분 출력
        System.out.println(deque.removeFirst()); // 3
        System.out.println(deque); // [2, 1, 10, 20, 30]

        // Rear 부분 출력
        System.out.println(deque.removeLast()); // 30
        System.out.println(deque); // [2, 1, 10, 20]

        System.out.println(deque.removeLast()); // 20
        System.out.println(deque.removeLast()); // 10
        System.out.println(deque.removeLast()); // 1
        System.out.println(deque.removeLast()); // 2
        System.out.println(deque); // []

        System.out.println(deque.pollLast()); // null
        System.out.println(deque.removeLast()); // 예외 발생
    }
}

연산 종류

앞쪽에서의 삽입 (addFirst) 및 뒤쪽에서의 삽입 (addLast)
앞쪽에서의 삭제 (removeFirst) 및 뒤쪽에서의 삭제 (removeLast)
앞쪽의 요소 확인 (getFirst) 및 뒤쪽의 요소 확인 (getLast)
비어 있는지 확인 (isEmpty)
가득 찼는지 확인 (isFull)

'알고리즘 & 자료구조 > 자료구조' 카테고리의 다른 글

비선형 자료구조 - 힙(Heap) (0)	2024.08.23
선형 자료구조 - 해시 테이블(Hash Table) (0)	2024.08.22
선형 자료구조 - 큐(Queue) (0)	2024.08.19
선형 자료구조 - 스택(Stack) (0)	2024.08.17
선형 자료구조 - 연결 리스트(Linked List) (0)	2024.08.17

현재글선형 자료구조 - 데크(Deque)

개발공부일지

개발공부기록

최단 경로 알고리즘, 메서드 선언, 비선형자료구조, 항해99, 기본편, 비선형 자료구조, 개발자취업, 자바의 기초, 인프런, til, 99클럽, 선형자료구조, 김영한의 자바, 오블완, 선형 자료구조, 티스토리챌린지, 코딩테스트준비, 알고리즘, 기본형, Java,

Today :
Yesterday :

일	월	화	수	목	금	토
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

개발공부일지