그래프(Graph)
- 정점과 간선으로 이루어진 (Cyclic) (트리와 차이점=> 트리는 Cyclic X)
- 연결된 정점간의 관계를 표혀할 수 있는 자료구조
- 그래프의 용도
- 지하철 노선도, 통신 네트워크, ...
그래프 구조
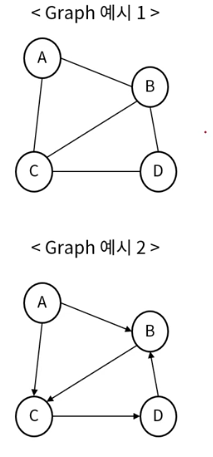
- 정점(Vertex): 각 노드
- 간선(Edge): 노드와 노드를 연결하는 선(ink, breanch)
- 인접 정점(Adjacent vertex): 간선 하나를 두고 바로 연결된 정점
- 정점의 차수(Degree):
- 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 무방향 그래프 모든 정점 차수의 합 = 그래프 간선의 수 2배
- 진입 차수(In-dgree): 방향 그래프에서 외부에서 오는 간전의 수
- 진출 차수(Out-dgree): 방향 그래프에서 외부로 나가는 간선의 수
- 경로 길이(Path length): 경로를 궝하는데 사용된 간선의 수
- 단순 경로(Simple path): 경로 중에서 반복되는 정점이 없는 경우
- 사이클(Cycle): 단순 경로의 시작 정점과 끝 정점이 동일한 경우
그래프의 특징과 트리와의 차이
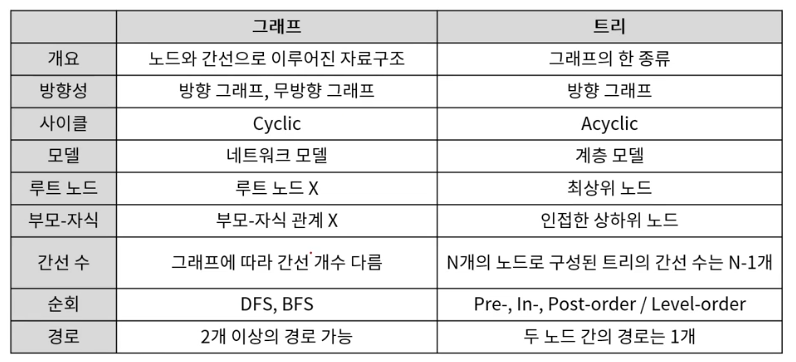
그래프의 종류
- 무방향 그래프
- 간선에 방향이 없는 그래프 (양방향 이동 가능)
- 정점 A-B 간선의 표현: (A, B) = (B, A)
- 방향 그래프
- 간선에 방향이 있는 그래프(해당 방향으로만 이동 가능)
- 정점 A-> B간선의 표현: < A, B > != < B, A >
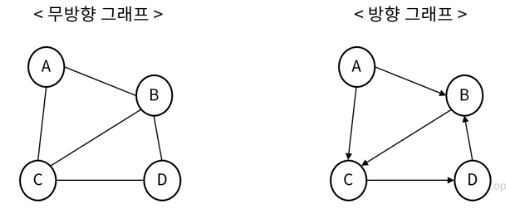
- 가중치 그래프
- 간선에 값이 있는 그래프 (이동 비용)
- 완전 그래프
- 모든 정점이 서로 연결되어 있는 그래프
- 정점이 N개일 경우, 간선의 수는 n(n-1) / 2 개
그래프 탐색 - DFS
- 깊이 우선 탐색(Depth First Search)
- 각 노드에 방문했는지 여부를 체크할 배열과 스택 이용하여 구현
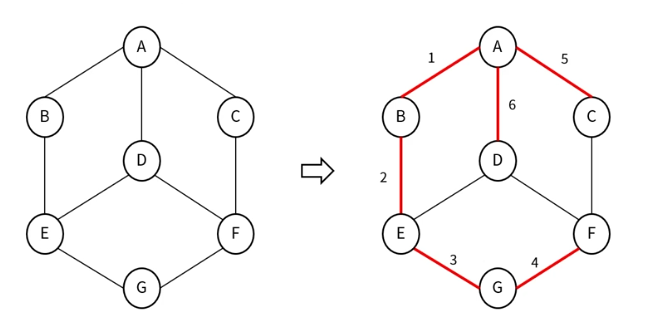
그래프 탐색 - BFS
- 너비 우선 탐색(Breath First Search)
- 각 노드에 방문했는지 여부를 체크할 배열과 큐 이용하여 구현
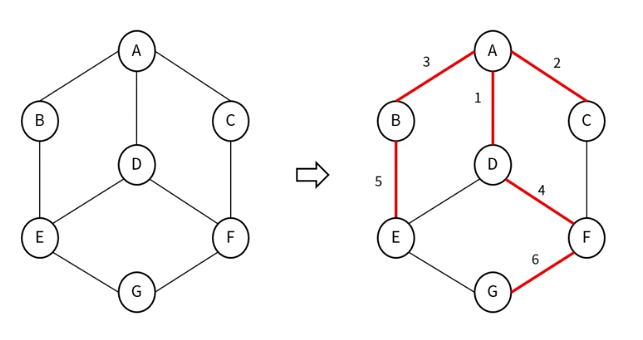
DFS, BFS 자바 코드 구현
인접 행렬
더보기
// Practice2
// 인접 행렬 그래프의 DFS, BFS
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
class MyGraphMatrix2 extends MyGraphMatrix {
public MyGraphMatrix2(int size) {
super(size);
}
public void dfs(int id) {
boolean[] visited = new boolean[this.elemCnt];
Stack<Integer> stack = new Stack<>();
stack.push(id);
visited[id] = true;
while (!stack.isEmpty()) {
int curId = stack.pop();
System.out.print(this.vertices[curId] + " ");
for (int i = this.elemCnt - 1; i >= 0; i--) {
if (this.adjMat[curId][i] == 1 && visited[i] == false) {
stack.push(i);
visited[i] = true;
}
}
}
System.out.println();
}
public void bfs(int id) {
boolean[] visited = new boolean[this.elemCnt];
Queue<Integer> queue = new LinkedList<>();
queue.offer(id);
visited[id] = true;
while (!queue.isEmpty()) {
int curId = queue.poll();
System.out.print(this.vertices[curId] + " ");
for (int i = this.elemCnt - 1; i >= 0; i--) {
if (this.adjMat[curId][i] == 1 && visited[i] == false) {
queue.offer(i);
visited[i] = true;
}
}
}
System.out.println();
}
}
public class Practice2 {
public static void main(String[] args) {
// Test code
MyGraphMatrix2 graph = new MyGraphMatrix2(7);
graph.addVertex('A'); // 0
graph.addVertex('B'); // 1
graph.addVertex('C'); // 2
graph.addVertex('D'); // 3
graph.addVertex('E'); // 4
graph.addVertex('F'); // 5
graph.addVertex('G'); // 6
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(0, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 5);
graph.addEdge(3, 4);
graph.addEdge(3, 5);
graph.addEdge(4, 6);
graph.addEdge(5, 6);
graph.printAdjacentMatrix();
graph.dfs(0);
graph.bfs(0);
}
}
A B C D E F G
A 0 1 1 1 0 0 0
B 1 0 0 0 1 0 0
C 1 0 0 0 0 1 0
D 1 0 0 0 1 1 0
E 0 1 0 1 0 0 1
F 0 0 1 1 0 0 1
G 0 0 0 0 1 1 0
A B E G F C D
A D C B F E G
인접 리스트
더보기
// Practice3
// 인접 리스트 그래프의 DFS, BFS
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
class MyGraphList2 extends MyGraphList {
public MyGraphList2(int size) {
super(size);
}
public void dfs(int id) {
boolean[] visited = new boolean[this.elemCnt];
Stack<Integer> stack = new Stack<>();
stack.push(id);
visited[id] = true;
while (!stack.isEmpty()) {
int curId = stack.pop();
System.out.print(this.vertices[curId] + " ");
Node cur = this.adjList[curId];
while (cur != null) {
if (visited[cur.id] == false) {
stack.push(cur.id);
visited[cur.id] = true;
}
cur = cur.next;
}
}
System.out.println();
}
public void bfs(int id) {
boolean[] visited = new boolean[this.elemCnt];
Queue<Integer> queue = new LinkedList<>();
queue.offer(id);
visited[id] = true;
while (!queue.isEmpty()) {
int curId = queue.poll();
System.out.print(this.vertices[curId] + " ");
Node cur = this.adjList[curId];
while (cur != null) {
if (visited[cur.id] == false) {
queue.offer(cur.id);
visited[cur.id] = true;
}
cur = cur.next;
}
}
System.out.println();
}
}
public class Practice3 {
public static void main(String[] args) {
// Test code
MyGraphList2 graph = new MyGraphList2(7);
graph.addVertex('A'); // 0
graph.addVertex('B'); // 1
graph.addVertex('C'); // 2
graph.addVertex('D'); // 3
graph.addVertex('E'); // 4
graph.addVertex('F'); // 5
graph.addVertex('G'); // 6
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(0, 3);
graph.addEdge(1, 4);
graph.addEdge(2, 5);
graph.addEdge(3, 4);
graph.addEdge(3, 5);
graph.addEdge(4, 6);
graph.addEdge(5, 6);
graph.printAdjacentList();
graph.dfs(0);
graph.bfs(0);
}
}
A: D C B
B: E A
C: F A
D: F E A
E: G D B
F: G D C
G: F E
A B E G F C D
A D C B F E G
그래프 구현
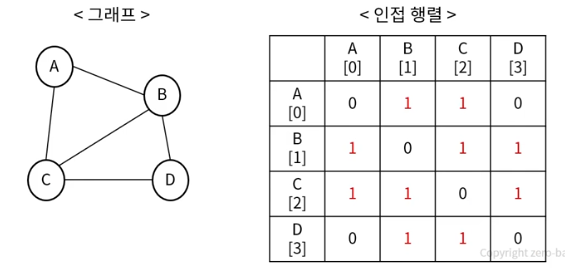
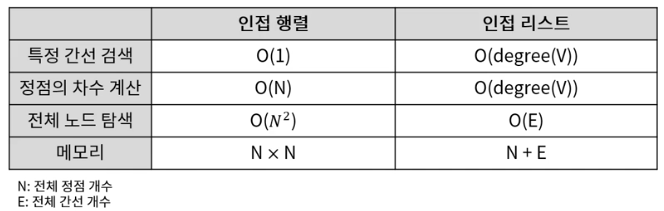
- 인접 행렬(Adjacency Matrix)
- 2차원 배열 이용
- 인접 행렬의 장단점
- 간선 정보의 확인과 업데이트가 빠름 O(1)
- 인접 행렬을 위한 메모리 공간 차지
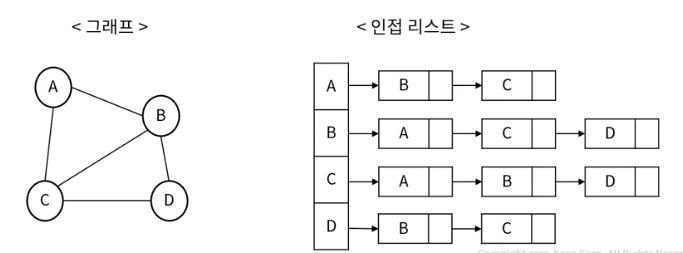
- 인접 리스트(Adjacency List)
- 연결리스트 이용
- 인접 리스트의 장단점
- 메모리 사용량이 상대적으로 적고, 노드의 추가 삭제 빠름
- 간선 정보 확인이 상대적으로 오래 걸림
인접 행렬 vs 인접 리스트
- 인접 행렬
- 노드의 개수가 적고 간선의수가 많을 때 유리 // 밀집 그래프(Dense Graph)
- 인접 리스트
- 노드의 개수가 많고 간선의수가 적을 때 유리 // 희소 그래프(Sparse Graph)
그래프 코드 구현
인접 행렬 (무방향, 방향 그래프)
// 비선형 자료구조 - 그래프
// 인접 행렬을 이용한 그래프 구현
class MyGraphMatrix {
char[] vertices; // 알파벳 담을 변수
int[][] adjMat; // 2차원 인접 행렬
int elemCnt; // 정점 갯수 카운트
public MyGraphMatrix() {
}
public MyGraphMatrix(int size) {
this.vertices = new char[size];
this.adjMat = new int[size][size];
this.elemCnt = 0;
}
public boolean isFull() {
return this.elemCnt == this.vertices.length;
}
public void addVertex(char data) {
if (isFull()) {
System.out.println("Graph is full");
return;
}
this.vertices[this.elemCnt++] = data;
}
// 무방향 그래프
public void addEdge(int x, int y) {
this.adjMat[x][y] = 1;
this.adjMat[y][x] = 1;
}
// 방향 그래프
public void addDirectedEdge(int x, int y) {
this.adjMat[x][y] = 1;
}
// 무방향 그래프
public void deleteEdge(int x, int y) {
this.adjMat[x][y] = 0;
this.adjMat[y][x] = 0;
}
// 방향 그래프
public void deleteDirectedEdge(int x, int y) {
this.adjMat[x][y] = 0;
}
public void printAdjacentMatrix() {
System.out.print(" ");
for (char item : this.vertices) {
System.out.print(item + " ");
}
System.out.println();
for (int i = 0; i < this.elemCnt; i++) {
System.out.print(this.vertices[i] + " ");
for (int j = 0; j < this.elemCnt; j++) {
System.out.print(this.adjMat[i][j]+" ");
}
System.out.println();
}
}
}
public class Main {
public static void main(String[] args) {
// Test code
MyGraphMatrix graph = new MyGraphMatrix(4);
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 3);
graph.printAdjacentMatrix();
// A B C D
// A 0 1 1 0
// B 1 0 1 1
// C 1 1 0 1
// D 0 1 1 0
}
}
인접 리스트
// Practice1
// 인접 리스트를 이용한 그래프 구현
class Node {
int id;
Node next;
public Node(int id, Node next) {
this.id = id;
this.next = next;
}
}
class MyGraphList {
char[] vertices;
Node[] adjList;
int elemCnt;
public MyGraphList(){}
public MyGraphList(int size) {
this.vertices = new char[size];
this.adjList = new Node[size];
this.elemCnt = 0;
}
public boolean isFull() {
return this.elemCnt == this.vertices.length;
}
public void addVertex(char data) {
if (isFull()) {
System.out.println("Graph is Full!");
return;
}
this.vertices[elemCnt++] = data;
}
// 각 데이터에 연결 노드들을 앞쪽으로 추가하는 방식(next 링크 수정이 번거로우니)
public void addEdge(int x, int y) {
this.adjList[x] = new Node(y, this.adjList[x]);
this.adjList[y] = new Node(x, this.adjList[y]);
}
public void addDirectedEdge(int x, int y) {
this.adjList[x] = new Node(y, this.adjList[x]);
}
public void printAdjacentList() {
for (int i = 0; i < this.elemCnt; i++) {
System.out.print(this.vertices[i] + ": ");
Node cur = this.adjList[i];
while (cur != null) {
System.out.print(this.vertices[cur.id] + " ");
cur = cur.next;
}
System.out.println();
}
}
}
public class Practice1 {
public static void main(String[] args) {
// Test code
MyGraphList graph = new MyGraphList(4);
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 3);
graph.printAdjacentList();
// A: C B
// B: D C A
// C: D B A
// D: C B
}
}
'알고리즘 & 자료구조 > 자료구조' 카테고리의 다른 글
| 비선형 자료구조 - 트라이(Trie) (0) | 2024.09.05 |
|---|---|
| 비선형 자료구조 - 우선순위 큐(Priority Queue) (0) | 2024.08.31 |
| 비선형 자료구조 - 힙(Heap) (0) | 2024.08.23 |
| 선형 자료구조 - 해시 테이블(Hash Table) (0) | 2024.08.22 |
| 선형 자료구조 - 데크(Deque) (0) | 2024.08.20 |