문제 1)

- 이진탐색을 이용하여 아래의 그림과 같이 최솟값 최댓값 사이의 중앙값을 구하여 2개(n개)의 제거를 만족하는 최솟값 중에 최댓값 구해보기
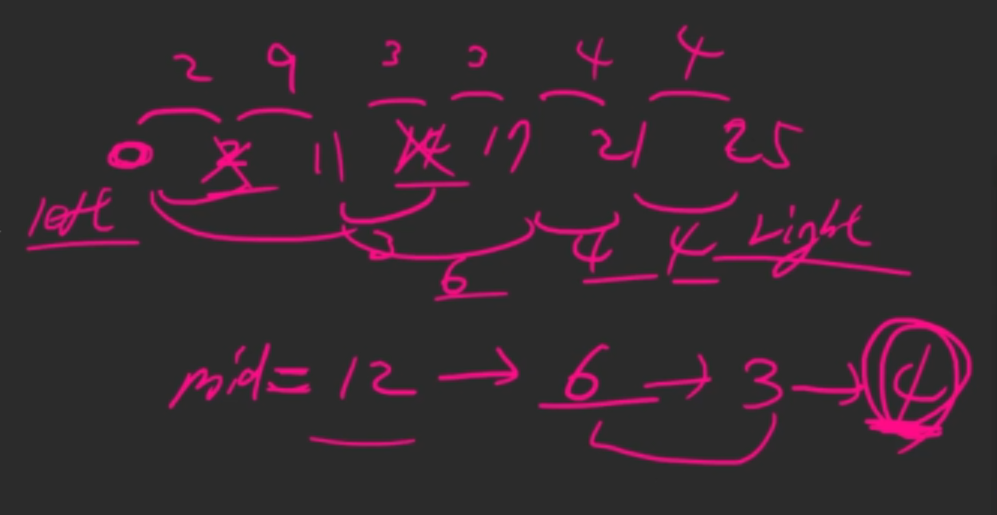
import java.util.Arrays;
public class Practice1 {
public static int solution(int[] rocks, int goal, int n) {
if (rocks == null || rocks.length == 0) {
return -1;
}
Arrays.sort(rocks);
// 바위를 n 개 지웠을 때 최소 step 중 max 값을 찾는 문제
int left = 0;
int right = goal;
int result = Integer.MIN_VALUE; // 최솟값 중에서 최댓값 구하기
while (left <= right) {
int mid = (left + right) / 2;
int cnt = 0; // 돌 제거 갯수 카운팅 변수
int prev = 0; // 제거되지 않은 이전 돌의 위치(제거되면 그 돌은 날리면 됨)
// mid 간격 보다 돌 사이 간격이 작으면 제거
// 그렇지 않으면 pass
for (int i = 0; i < rocks.length; i++) {
if (rocks[i] - prev < mid) {
cnt++; // 돌 제거
} else {
prev = rocks[i];
}
if (cnt > n) {
break;
}
}
// 최종 위치와의 간격도 계산
if (goal - prev < mid && cnt <= n) {
cnt++;
}
// n 개 보다 많이 제거 했으면, right 간격을 줄여서 반복
// n 개 보다 적게 재거 했으면, left 간격을 늘려서 반복
if (cnt > n) {
right = mid - 1;
} else {
left = mid + 1;
if (cnt == n) {
result = Math.max(result, mid);
}
}
}
return result;
}
public static void main(String[] args) {
// Test code
int[] rocks = {11, 2, 14, 21, 17};
int goal = 25;
int n = 2;
System.out.println(solution(rocks, goal, n));
}
}
4문제 2)

- Answer: 실제 무게 / Expectation: 예상 무게
- 투포인터를 이용하여 문제의 답 구하기
- 투포인터를 0번 부터 시작하여 A^2 - E^2의 식을 이용
- 두 수의 차가 n보다 작으면 A를 오른쪽으로 이동 // 두 수의 차가 n보다 크면 E를 오른쪽으로 이동
import java.util.ArrayList;
public class Practice2 {
public static void solution(int n) {
int A = 1; // Answer의 포인터
int E = 1; // Expectation의 포인터
ArrayList result = new ArrayList();
while (true) {
// 실제 무게 제곱 - 예상 무게 제곱
int diff = A * A - E * E;
if (A - E == 1 && diff > n) {
break;
}
// 두 수의 차가 작으면 A++
if (diff < n) {
A++;
} else { // 두 수의 차가 크면 E++
E++;
}
// 정답이 될 수 있는 case list 에 추가
if (diff == n) {
result.add(A);
}
}
if (result.size() != 0) {
System.out.println(result);
} else {
System.out.println(-1);
}
}
public static void main(String[] args) {
// Test code
solution(15);
}
}
[4, 8]문제 3)

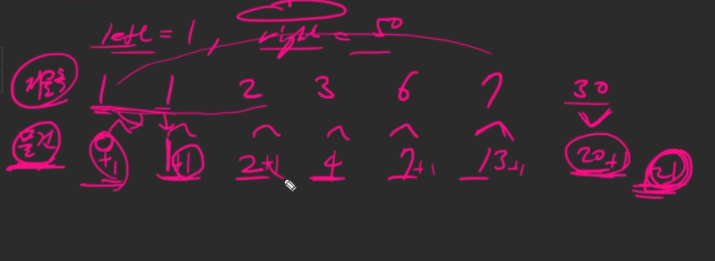
- 규칙을 발견해야 함 => 각 배열을 오름차순으로 정렬한 후
- 현재까지의 누적 저울추들의 합이 그 해당 인덱스의 저울추보다 큰 값인지
- 현재까지의 누적 저울추들의 합에 +1 한 값을 만들 수 있는지 두 가지 경우를 충족하지 않는 수를 찾아야 함
import java.util.Arrays;
public class Practice3 {
public static int solution(int[] weights) {
// 우선 무게 순으로 오름차순 정렬
Arrays.sort(weights);
int cur = 0;
for (int i = 0; i < weights.length; i++) {
// 현재 무게 + 1이 그 다음 저울 추의 무게보다 작을 때 더 이상 측정 불가
if (cur + 1 < weights[i]) {
break;
}
cur += weights[i];
}
return cur + 1;
}
public static void main(String[] args) {
// Test code
int[] weights = {6, 1, 2, 3, 1, 7, 30};
System.out.println(solution(weights));
}
}
21문제 4)
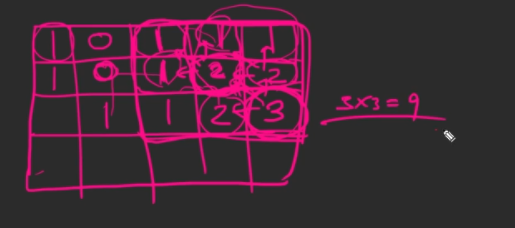
- DP 방식으로 문제 풀이
public class Practice4 {
public static int solution(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return -1;
}
int maxVal = 0;
// 정사각형 구하므로 위 아래로 인접한 두 줄만 있으면 가능하므로 2행 x 열 길이 만큼만 dp 테이블 생성
int[][] dp = new int[2][matrix[0].length];
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
dp[i % 2][j] = matrix[i][j];
// 첫 행, 첫 열이 아니고 현재 위치가 0 이 아닐 때
if (i != 0 && j != 0 && dp[i % 2][j] != 0) {
int up = dp[i % 2][j - 1];
int left = dp[(i - 1) % 2][j];
int ul = dp[(i - 1) % 2][j - 1]; // 위의 왼쪽 변수
// 인접한 정사각 형 구역 중 최소 값 구해서 1 증가
int minVal = Math.min(Math.min(up, left), ul);
dp[i % 2][j] = minVal + 1;
}
maxVal = Math.max(maxVal, dp[i % 2][j]);
}
}
return maxVal * maxVal;
}
public static void main(String[] args) {
// Test code
int[][] data = {{0, 1}, {1, 0}};
System.out.println(solution(data));
data = new int[][]{{1, 0, 1, 1, 1}, {1, 0, 1, 1, 1}, {1, 1, 1, 1, 1}, {1, 0, 1, 1, 0}};
System.out.println(solution(data));
}
}
1
9문제 5)

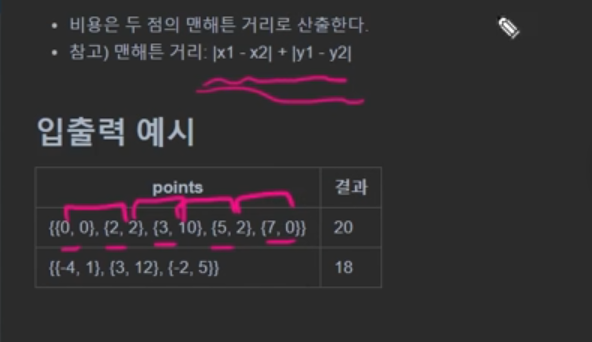
- 각 노드들 간의 맨해튼 거리 구하면 됨
import java.util.PriorityQueue;
public class Practice5 {
static class Node {
int idx;
int weight;
public Node(int idx, int weight) {
this.idx = idx;
this.weight = weight;
}
}
static boolean[] visited;
public static int solution(int[][] points) {
visited = new boolean[points.length];
PriorityQueue<Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
pq.offer(new Node(0, 0));
int weightSum = 0;
int cnt = 0;
while (cnt < points.length) {
Node cur = pq.poll();
if (visited[cur.idx]) {
continue;
}
visited[cur.idx] = true;
weightSum += cur.weight;
cnt++;
// 인접한 점들과의 거리 계산하여 pq에 추가
for (int i = 0; i < points.length; i++) {
// 동일 노드 제외
if (i == cur.idx) {
continue;
}
// 맨해튼 거리
int distance =
Math.abs(points[i][0] - points[cur.idx][0]) + Math.abs(points[i][1] - points[cur.idx][1]);
pq.add(new Node(i, distance));
}
}
return weightSum;
}
public static void main(String[] args) {
// Test code
int[][] points = {{0, 0}, {2, 2}, {3, 10}, {5, 2}, {7, 0}};
System.out.println(solution(points));
points = new int[][]{{-4, 1}, {3, 12}, {-2, 5}};
System.out.println(solution(points));
}
}
20
18'개발 공부 > 문제와 풀이' 카테고리의 다른 글
| 비선형 자료구조 - 트라이 연습문제 (1) | 2024.09.06 |
|---|---|
| 알고리즘 - 연습 문제 1 (2) | 2024.09.04 |
| 최단 경로 알고리즘 - 연습 문제 (1) | 2024.09.02 |
| 해시테이블 - 연습 문제 (7) | 2024.08.28 |
| 연결 리스트 - 연습 문제 4 (2) | 2024.08.28 |